Найти условный. Наибольшее и наименьшее значение функции в замкнутой области

Экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Условный экстремум. Метод множителей Лагранжа. Нахождение наибольших и наименьших значений.

Лекция 5.

Определение 5.1. Точка М 0 (х 0 , у 0) называется точкой максимума функции z = f (x, y), если f (x o , y o) > f (x, y) для всех точек (х, у) М 0 .

Определение 5.2. Точка М 0 (х 0 , у 0) называется точкой минимума функции z = f (x, y), если f (x o , y o) < f (x, y) для всех точек (х, у) из некоторой окрестности точки М 0 .

Замечание 1. Точки максимума и минимума называются точками экстремума функции нескольких переменных.

Замечание 2. Аналогичным образом определяется точка экстремума для функции от любого количества переменных.

Теорема 5.1 (необходимые условия экстремума). Если М 0 (х 0 , у 0) – точка экстремума функции z = f (x, y), то в этой точке частные производные первого порядка данной функции равны нулю или не существуют.

Доказательство.

Зафиксируем значение переменной у , считая у = у 0 . Тогда функция f (x, y 0) будет функцией одной переменной х , для которой х = х 0 является точкой экстремума. Следовательно, по теореме Ферма или не существует. Аналогично доказывается такое же утверждение для .

Определение 5.3. Точки, принадлежащие области определения функции нескольких переменных, в которых частные производные функции равны нулю или не существуют, называются стационарными точками этой функции.

Замечание. Таким образом, экстремум может достигаться только в стационарных точках, но не обязательно он наблюдается в каждой из них.

Теорема 5.2 (достаточные условия экстремума). Пусть в некоторой окрестности точки М 0 (х 0 , у 0) , являющейся стационарной точкой функции z = f (x, y), эта функция имеет непрерывные частные производные до 3-го порядка включительно. Обозначим Тогда:

1) f (x, y) имеет в точке М 0 максимум, если AC – B ² > 0, A < 0;

2) f (x, y) имеет в точке М 0 минимум, если AC – B ² > 0, A > 0;

3) экстремум в критической точке отсутствует, если AC – B ² < 0;

4) если AC – B ² = 0, необходимо дополнительное исследование.

Доказательство.

Напишем формулу Тейлора второго порядка для функции f (x, y), помня о том, что в стационарной точке частные производные первого порядка равны нулю:

где Если угол между отрезком М 0 М , где М (х 0 + Δх, у 0 + Δу ), и осью Ох обозначить φ, то Δх = Δρ cosφ, Δy = Δρsinφ. При этом формула Тейлора примет вид: . Пусть Тогда можно разделить и умножить выражение в скобках на А . Получим:

Рассмотрим теперь четыре возможных случая:

1) AC-B ² > 0, A < 0. Тогда , и при достаточно малых Δρ. Следовательно, в некоторой окрестности М 0 f (x 0 + Δx, y 0 + Δy) < f (x 0 , y 0) , то есть М 0 – точка максимума.

2) Пусть AC – B ² > 0, A > 0. Тогда , и М 0 – точка минимума.

3) Пусть AC-B ² < 0, A > 0. Рассмотрим приращение аргументов вдоль луча φ = 0. Тогда из (5.1) следует, что , то есть при движении вдоль этого луча функция возрастает. Если же перемещаться вдоль луча такого, что tg φ 0 = -A/B, то , следовательно, при движении вдоль этого луча функция убывает. Значит, точка М 0 не является точкой экстремума.

3`) При AC – B ² < 0, A < 0 доказательство отсутствия экстремума проводится

аналогично предыдущему.

3``) Если AC – B ² < 0, A = 0, то . При этом . Тогда при достаточно малых φ выражение 2B cosφ + C sinφ близко к 2В , то есть сохраняет постоянный знак, а sinφ меняет знак в окрестности точки М 0 . Значит, приращение функции меняет знак в окрестности стационарной точки, которая поэтому не является точкой экстремума.

4) Если AC – B ² = 0, а , , то есть знак приращения определяется знаком 2α 0 . При этом для выяснения вопроса о существовании экстремума необходимо дальнейшее исследование.

Пример. Найдем точки экстремума функции z = x ² - 2xy + 2y ² + 2x. Для поиска стационарных точек решим систему . Итак, стационарная точка (-2,-1). При этом А = 2, В = -2, С = 4. Тогда AC – B ² = 4 > 0, следовательно, в стационарной точке достигается экстремум, а именно минимум (так как A > 0).

Определение 5.4. Если аргументы функции f (x 1 , x 2 ,…, x n) связаны дополнительными условиями в виде m уравнений (m < n) :

φ 1 (х 1 , х 2 ,…, х n) = 0, φ 2 (х 1 , х 2 ,…, х n) = 0, …, φ m (х 1 , х 2 ,…, х n) = 0, (5.2)

где функции φ i имеют непрерывные частные производные, то уравнения (5.2) называются уравнениями связи .

Определение 5.5. Экстремум функции f (x 1 , x 2 ,…, x n) при выполнении условий (5.2) называется условным экстремумом .

Замечание. Можно предложить следующее геометрическое истолкование условного экстремума функции двух переменных: пусть аргументы функции f(x,y) связаны уравнением φ(х,у) = 0, задающим некоторую кривую в плоскости Оху . Восставив из каждой точки этой кривой перпендикуляры к плоскости Оху до пересечения с поверхностью z = f (x,y), получим пространственную кривую, лежащую на поверхности над кривой φ(х,у) = 0. Задача состоит в поиске точек экстремума полученной кривой, которые, разумеется, в общем случае не совпадают с точками безусловного экстремума функции f(x,y).

Определим необходимые условия условного экстремума для функции двух переменных, введя предварительно следующее определение:

Определение 5.6. Функция L (x 1 , x 2 ,…, x n) = f (x 1 , x 2 ,…, x n) + λ 1 φ 1 (x 1 , x 2 ,…, x n) +

+ λ 2 φ 2 (x 1 , x 2 ,…, x n) +…+λ m φ m (x 1 , x 2 ,…, x n) , (5.3)

где λ i – некоторые постоянные, называется функцией Лагранжа , а числа λ i – неопределенными множителями Лагранжа .

Теорема 5.3 (необходимые условия условного экстремума). Условный экстремум функции z = f (x, y) при наличии уравнения связи φ (х, у) = 0 может достигаться только в стационарных точках функции Лагранжа L (x, y) = f (x, y) + λφ (x, y).

Доказательство. Уравнение связи задает неявную зависимость у от х , поэтому будем считать, что у есть функция от х : у = у(х). Тогда z есть сложная функция от х , и ее критические точки определяются условием: . (5.4) Из уравнения связи следует, что . (5.5)

Умножим равенство (5.5) на некоторое число λ и сложим с (5.4). Получим:

, или .

Последнее равенство должно выполняться в стационарных точках, откуда следует:

(5.6)

Получена система трех уравнений относительно трех неизвестных: х, у и λ, причем первые два уравнения являются условиями стационарной точки функции Лагранжа. Исключая из системы (5.6) вспомогательное неизвестное λ, находим координаты точек, в которых исходная функция может иметь условный экстремум.

Замечание 1. Проверку наличия условного экстремума в найденной точке можно провести с помощью исследования частных производных второго порядка функции Лагранжа по аналогии с теоремой 5.2.

Замечание 2. Точки, в которых может достигаться условный экстремум функции f (x 1 , x 2 ,…, x n) при выполнении условий (5.2), можно определить как решения системы (5.7)

Пример. Найдем условный экстремум функции z = xy при условии х + у = 1. Составим функцию Лагранжа L(x, y) = xy + λ (x + y – 1). Система (5.6) при этом выглядит так:

Откуда -2λ=1, λ=-0,5, х = у = -λ = 0,5. При этом L (x, y) можно представить в виде L (x, y) = - 0,5 (x – y )² + 0,5 ≤ 0,5, поэтому в найденной стационарной точке L (x, y) имеет максимум, а z = xy – условный максимум.

Достаточное условие экстремума функции двух переменных

1. Пусть функция непрерывно дифференцируема в некоторой окрестности точки и имеет непрерывные частные производные второго порядка (чистые и смешанные).

2. Обозначим за определитель второго порядка

экстремум переменная лекционный функция

Теорема

Если точка с координатами является стационарной точкой для функции, то:

А) При она является точкой локального экстремума причем, при локального максимума, - локального минимума;

В) при точка не является точкой локального экстремума;

С) если, может быть и то, и другое.

Доказательство

Запишем формулу Тейлора для функции, ограничившись двумя членами:

Так как по условию теоремы точка является стационарной, то частные производные второго порядка равны нулю, т.е. и. Тогда

Обозначим

Тогда приращение функции примет вид:

В силу непрерывности частных производных второго порядка (чистых и смешанных) по условию теоремы в точке можно записать:

Где или; ,

1. Пусть и, т.е. или.

2. Приращение функции умножим и разделим на, получим:

3. Дополним выражение в фигурных скобках до полного квадрата суммы:

4. Выражение в фигурных скобках неотрицательно, так как

5. Поэтому если а значит, и, то и, следовательно, согласно определению, точка является точкой локального минимума.

6. Если а значит, и, то, согласно определению точка с координатами - точка локального максимума.

2. Рассмотрим квадратный трехчлен, его дискриминант, .

3. Если, то существуют такие точки, что многочлен

4. Полное приращение функции в точке в соответствии с выражением, полученным в I, запишем в виде:

5. В силу непрерывности частных производных второго порядка по условию теоремы в точке можно записать, что

следовательно, существует - окрестность точки, что, для любой точки квадратный трехчлен больше нуля:

6. Рассмотрим - окрестность точки.

Выберем любое значение, так что точка. Полагая, что в формуле приращения функции

Что, получим:

7. Так как, то.

8. Рассуждая аналогично для корня, получим, что в любой -окрестности точки существует точка для которой, следовательно, в окрестности точки не сохраняет знак, следовательно в точке экстремума нет.

Условный экстремум функции двух переменных

При отыскании экстремумов функции двух переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных.

Пусть заданы функция и линия L на плоскости 0xy. Задача состоит в том, чтобы на линии L найти такую точку P (x, y), в которой значение функции является наибольшим или наименьшим по сравнению со значениями этой функции в точках линии L, находящихся вблизи точки P. Такие точки P называются точками условного экстремума функции на линии L. В отличие от обычной точки экстремума значение функции в точке условного экстремума сравнивается со значениями функции не во всех точках некоторой ее окрестности, а только в тех, которые лежат на линии L.

Совершенно ясно, что точка обычного экстремума (говорят также безусловного экстремума) является и точкой условного экстремума для любой линии, проходящей через эту точку. Обратное же, разумеется, неверно: точка условного экстремума может и не быть точкой обычного экстремума. Проиллюстрируем сказанное на примере.

Пример №1. Графиком функции является верхняя полусфера (рис. 2).

Рис. 2.

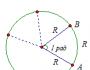
Эта функция имеет максимум в начале координат; ему соответствует вершина M полусферы. Если линия L есть прямая, проходящая через точки А и В (ее уравнение), то геометрически ясно, что для точек этой линии наибольшее значение функции достигается в точке, лежащей посередине между точками А и В. Это и есть точка условного экстремума (максимума) функции на данной линии; ей соответствует точка M 1 на полусфере, и из рисунка видно, что ни о каком обычном экстремуме здесь не может быть речи.

Отметим, что в заключительной части задачи об отыскании наибольшего и наименьшего значений функции в замкнутой области приходится находить экстремальные значения функции на границе этой области, т.е. на какой-то линии, и тем самым решать задачу на условный экстремум.

Определение 1. Говорят, что, где имеет в точке, удовлетворяющей уравнению, условный или относительный максимум (минимум): если для любой, удовлетворяющей уравнению, выполняется неравенство

Определение 2. Уравнение вида называется уравнением связи.

Теорема

Если функции и непрерывно дифференцируемы в окрестности точки, и частная производная, и точка является точкой условного экстремума функции относительно уравнения связи, то определитель второго порядка равен нулю:

Доказательство

1. Так как по условию теоремы частная производная, а значение функции, то в некотором прямоугольнике

определена неявная функция

Сложная функция двух переменных в точке будет иметь локальный экстремум, следовательно, или.

2. Действительно, согласно свойству инвариантности формулы дифференциала первого порядка

3. Уравнение связи можно представить в таком виде, значит

4. Умножим уравнение (2) на, а (3) на и сложим их

Следовательно, при

произвольном. ч.т.д.

Следствие

Поиск точек условного экстремума функции двух переменных на практике осуществляется путем решения системы уравнений

Так, в вышеприведенном примере №1 из уравнения связи имеем. Отсюда легко проверить, что достигает максимума при. Но тогда из уравнения связи. Получаем точку P, найденную геометрически.

Пример №2. Найти точки условного экстремума функции относительно уравнения связи.

Найдем частные производные заданной функции и уравнения связи:

Составим определитель второго порядка:

Запишем систему уравнений для отыскания точек условного экстремума:

значит, существует четыре точки условного экстремума функции с координатами: .

Пример №3. Найти точки экстремума функции.

Приравнивая частные производные к нулю: , находим одну стационарную точку - начало координат. Здесь,. Следовательно, и точка (0, 0) не является точкой экстремума. Уравнение есть уравнение гиперболического параболоида (Рис. 3) по рисунку видно, что точка (0, 0) не является точкой экстремума.

Рис. 3.

Наибольшее и наименьшее значение функции в замкнутой области

1. Пусть функция определена и непрерывна в ограниченной замкнутой области D.

2. Пусть в этой области функция имеет конечные частные производные, кроме отдельных точек области.

3. В соответствии с теоремой Вейерштрасса в этой области найдется точка, в которой функция примет наибольшее и наименьшее значение.

4. Если эти точки будут внутренними точками области D, то очевидно, в них будет максимум или минимум.

5. В этом случае интересующие нас точки находятся среди подозрительных точек на экстремум.

6. Однако наибольшее или наименьшее значение функция может принимать и на границе области D.

7. Для того, чтобы найти наибольшее (наименьшее) значение функции в области D, нужно найти все внутренние точки подозрительные на экстремум, вычислить значение функции в них, затем сравнить со значением функции в пограничных точках области, и наибольшее из всех найденных значений будет являться наибольшим в замкнутой области D.

8. Метод отыскания локального максимума или минимума рассматривался ранее в п. 1.2. и 1.3.

9. Остается рассмотреть метод отыскания наибольшего и наименьшего значения функции на границе области.

10. В случае функции двух переменных область обычно оказывается ограниченной кривой или нескольких кривыми.

11. Вдоль такой кривой (или нескольких кривых) переменные и либо зависят одна от другой, либо обе зависят от одного параметра.

12. Таким образом, на границе функция оказывается зависящей от одной переменной.

13. Метод отыскания наибольшего значения функции одной переменной был рассмотрен ранее.

14. Пусть граница области D задана параметрическими уравнениями:

Тогда на этой кривой функция двух переменных будет представлять собой сложную функцию от параметра: . Для такой функции наибольшее и наименьшее значение определяется по методике определения наибольшего и наименьшего значения для функции одной переменной.

Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $\varphi (x,y)=0$.

Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $\varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=\psi(x)$, то подставив $y=\psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=f\left(x,\psi(x)\right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.

Метод множителей Лагранжа для функций двух переменных.

Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ (параметр $\lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

$$ \left \{ \begin{aligned} & \frac{\partial F}{\partial x}=0;\\ & \frac{\partial F}{\partial y}=0;\\ & \varphi (x,y)=0. \end{aligned} \right. $$

Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_{xx}^{""}dx^2+2F_{xy}^{""}dxdy+F_{yy}^{""}dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F < 0$, то условный максимум.

Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: $\varphi_{x}^{"}dx+\varphi_{y}^{"}dy=0$, $dy=-\frac{\varphi_{x}^{"}}{\varphi_{y}^{"}}dx$, поэтому в любой стационарной точке имеем:

$$d^2 F=F_{xx}^{""}dx^2+2F_{xy}^{""}dxdy+F_{yy}^{""}dy^2=F_{xx}^{""}dx^2+2F_{xy}^{""}dx\left(-\frac{\varphi_{x}^{"}}{\varphi_{y}^{"}}dx\right)+F_{yy}^{""}\left(-\frac{\varphi_{x}^{"}}{\varphi_{y}^{"}}dx\right)^2=\\ =-\frac{dx^2}{\left(\varphi_{y}^{"} \right)^2}\cdot\left(-(\varphi_{y}^{"})^2 F_{xx}^{""}+2\varphi_{x}^{"}\varphi_{y}^{"}F_{xy}^{""}-(\varphi_{x}^{"})^2 F_{yy}^{""} \right)$$

Второй сомножитель (расположенный в скобке) можно представить в такой форме:

Красным цветом выделены элементы определителя $\left| \begin{array} {cc} F_{xx}^{""} & F_{xy}^{""} \\ F_{xy}^{""} & F_{yy}^{""} \end{array} \right|$, который является гессианом функции Лагранжа. Если $H > 0$, то $d^2F < 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F > 0$, т.е. имеем условный минимум функции $z=f(x,y)$.

Примечание относительно формы записи определителя $H$. показать\скрыть

$$ H=-\left|\begin{array} {ccc} 0 & \varphi_{x}^{"} & \varphi_{y}^{"}\\ \varphi_{x}^{"} & F_{xx}^{""} & F_{xy}^{""} \\ \varphi_{y}^{"} & F_{xy}^{""} & F_{yy}^{""} \end{array} \right| $$

В этой ситуации сформулированное выше правило изменится следующим образом: если $H > 0$, то функция имеет условный минимум, а при $H < 0$ получим условный максимум функции $z=f(x,y)$. При решении задач следует учитывать такие нюансы.

Алгоритм исследования функции двух переменных на условный экстремум

1. Составить функцию Лагранжа $F(x,y)=f(x,y)+\lambda\varphi(x,y)$
2. Решить систему $ \left \{ \begin{aligned} & \frac{\partial F}{\partial x}=0;\\ & \frac{\partial F}{\partial y}=0;\\ & \varphi (x,y)=0. \end{aligned} \right.$
3. Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:
   • Составить определитель $H$ и выяснить его знак
   • С учетом уравнения связи вычислить знак $d^2F$

Метод множителей Лагранжа для функций n переменных

Допустим, мы имеем функцию $n$ переменных $z=f(x_1,x_2,\ldots,x_n)$ и $m$ уравнений связи ($n > m$):

$$\varphi_1(x_1,x_2,\ldots,x_n)=0; \; \varphi_2(x_1,x_2,\ldots,x_n)=0,\ldots,\varphi_m(x_1,x_2,\ldots,x_n)=0.$$

Обозначив множители Лагранжа как $\lambda_1,\lambda_2,\ldots,\lambda_m$, составим функцию Лагранжа:

$$F(x_1,x_2,\ldots,x_n,\lambda_1,\lambda_2,\ldots,\lambda_m)=f+\lambda_1\varphi_1+\lambda_2\varphi_2+\ldots+\lambda_m\varphi_m$$

Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:

$$\left\{\begin{aligned} & \frac{\partial F}{\partial x_i}=0; (i=\overline{1,n})\\ & \varphi_j=0; (j=\overline{1,m}) \end{aligned} \right.$$

Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F < 0$, - то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

Определитель матрицы $\left| \begin{array} {ccccc} \frac{\partial^2F}{\partial x_{1}^{2}} & \frac{\partial^2F}{\partial x_{1}\partial x_{2}} & \frac{\partial^2F}{\partial x_{1}\partial x_{3}} &\ldots & \frac{\partial^2F}{\partial x_{1}\partial x_{n}}\\ \frac{\partial^2F}{\partial x_{2}\partial x_1} & \frac{\partial^2F}{\partial x_{2}^{2}} & \frac{\partial^2F}{\partial x_{2}\partial x_{3}} &\ldots & \frac{\partial^2F}{\partial x_{2}\partial x_{n}}\\ \frac{\partial^2F}{\partial x_{3} \partial x_{1}} & \frac{\partial^2F}{\partial x_{3}\partial x_{2}} & \frac{\partial^2F}{\partial x_{3}^{2}} &\ldots & \frac{\partial^2F}{\partial x_{3}\partial x_{n}}\\ \ldots & \ldots & \ldots &\ldots & \ldots\\ \frac{\partial^2F}{\partial x_{n}\partial x_{1}} & \frac{\partial^2F}{\partial x_{n}\partial x_{2}} & \frac{\partial^2F}{\partial x_{n}\partial x_{3}} &\ldots & \frac{\partial^2F}{\partial x_{n}^{2}}\\ \end{array} \right|$, выделенной в матрице $L$ красным цветом, есть гессиан функции Лагранжа. Используем следующее правило:

• Если знаки угловых миноров $H_{2m+1},\; H_{2m+2},\ldots,H_{m+n}$ матрицы $L$ совпадают с знаком $(-1)^m$, то исследуемая стационарная точка является точкой условного минимума функции $z=f(x_1,x_2,x_3,\ldots,x_n)$.
• Если знаки угловых миноров $H_{2m+1},\; H_{2m+2},\ldots,H_{m+n}$ чередуются, причём знак минора $H_{2m+1}$ совпадает с знаком числа $(-1)^{m+1}$, то исследуемая стационарная точка является точкой условного максимума функции $z=f(x_1,x_2,x_3,\ldots,x_n)$.

Пример №1

Найти условный экстремум функции $z(x,y)=x+3y$ при условии $x^2+y^2=10$.

Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости $z=x+3y$ для точек ее пересечения с цилиндром $x^2+y^2=10$.

Выразить одну переменную через другую из уравнения связи и подставить ее в функцию $z(x,y)=x+3y$ несколько затруднительно, поэтому будем использовать метод Лагранжа.

Обозначив $\varphi(x,y)=x^2+y^2-10$, составим функцию Лагранжа:

$$ F(x,y)=z(x,y)+\lambda \varphi(x,y)=x+3y+\lambda(x^2+y^2-10);\\ \frac{\partial F}{\partial x}=1+2\lambda x; \frac{\partial F}{\partial y}=3+2\lambda y. $$

Запишем систему уравнений для определения стационарных точек функции Лагранжа:

$$ \left \{ \begin{aligned} & 1+2\lambda x=0;\\ & 3+2\lambda y=0;\\ & x^2+y^2-10=0. \end{aligned} \right. $$

Если предположить $\lambda=0$, то первое уравнение станет таким: $1=0$. Полученное противоречие говорит о том, что $\lambda\neq 0$. При условии $\lambda\neq 0$ из первого и второго уравнений имеем: $x=-\frac{1}{2\lambda}$, $y=-\frac{3}{2\lambda}$. Подставляя полученные значения в третье уравнение, получим:

$$ \left(-\frac{1}{2\lambda} \right)^2+\left(-\frac{3}{2\lambda} \right)^2-10=0;\\ \frac{1}{4\lambda^2}+\frac{9}{4\lambda^2}=10; \lambda^2=\frac{1}{4}; \left[ \begin{aligned} & \lambda_1=-\frac{1}{2};\\ & \lambda_2=\frac{1}{2}. \end{aligned} \right.\\ \begin{aligned} & \lambda_1=-\frac{1}{2}; \; x_1=-\frac{1}{2\lambda_1}=1; \; y_1=-\frac{3}{2\lambda_1}=3;\\ & \lambda_2=\frac{1}{2}; \; x_2=-\frac{1}{2\lambda_2}=-1; \; y_2=-\frac{3}{2\lambda_2}=-3.\end{aligned} $$

Итак, система имеет два решения: $x_1=1;\; y_1=3;\; \lambda_1=-\frac{1}{2}$ и $x_2=-1;\; y_2=-3;\; \lambda_2=\frac{1}{2}$. Выясним характер экстремума в каждой стационарной точке: $M_1(1;3)$ и $M_2(-1;-3)$. Для этого вычислим определитель $H$ в каждой из точек.

$$ \varphi_{x}^{"}=2x;\; \varphi_{y}^{"}=2y;\; F_{xx}^{""}=2\lambda;\; F_{xy}^{""}=0;\; F_{yy}^{""}=2\lambda.\\ H=\left| \begin{array} {ccc} 0 & \varphi_{x}^{"} & \varphi_{y}^{"}\\ \varphi_{x}^{"} & F_{xx}^{""} & F_{xy}^{""} \\ \varphi_{y}^{"} & F_{xy}^{""} & F_{yy}^{""} \end{array} \right|= \left| \begin{array} {ccc} 0 & 2x & 2y\\ 2x & 2\lambda & 0 \\ 2y & 0 & 2\lambda \end{array} \right|= 8\cdot\left| \begin{array} {ccc} 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end{array} \right| $$

В точке $M_1(1;3)$ получим: $H=8\cdot\left| \begin{array} {ccc} 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end{array} \right|= 8\cdot\left| \begin{array} {ccc} 0 & 1 & 3\\ 1 & -1/2 & 0 \\ 3 & 0 & -1/2 \end{array} \right|=40 > 0$, поэтому в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_{\max}=z(1;3)=10$.

Аналогично, в точке $M_2(-1;-3)$ найдем: $H=8\cdot\left| \begin{array} {ccc} 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end{array} \right|= 8\cdot\left| \begin{array} {ccc} 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end{array} \right|=-40$. Так как $H < 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{\min}=z(-1;-3)=-10$.

Отмечу, что вместо вычисления значения определителя $H$ в каждой точке, гораздо удобнее раскрыть его в общем виде. Дабы не загромождать текст подробностями, этот способ скрою под примечание.

Запись определителя $H$ в общем виде. показать\скрыть

$$ H=8\cdot\left|\begin{array}{ccc}0&x&y\\x&\lambda&0\\y&0&\lambda\end{array}\right| =8\cdot\left(-\lambda{y^2}-\lambda{x^2}\right) =-8\lambda\cdot\left(y^2+x^2\right). $$

В принципе, уже очевидно, какой знак имеет $H$. Так как ни одна из точек $M_1$ или $M_2$ не совпадает с началом координат, то $y^2+x^2>0$. Следовательно, знак $H$ противоположен знаку $\lambda$. Можно и довести вычисления до конца:

$$ \begin{aligned} &H(M_1)=-8\cdot\left(-\frac{1}{2}\right)\cdot\left(3^2+1^2\right)=40;\\ &H(M_2)=-8\cdot\frac{1}{2}\cdot\left((-3)^2+(-1)^2\right)=-40. \end{aligned} $$

Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:

$$ d^2 F=F_{xx}^{""}dx^2+2F_{xy}^{""}dxdy+F_{yy}^{""}dy^2=2\lambda \left(dx^2+dy^2\right) $$

Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $\left(dx \right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $\lambda_1=-\frac{1}{2}$ получим $d^2F < 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

Ответ : в точке $(-1;-3)$ функция имеет условный минимум, $z_{\min}=-10$. В точке $(1;3)$ функция имеет условный максимум, $z_{\max}=10$

Пример №2

Найти условный экстремум функции $z(x,y)=3y^3+4x^2-xy$ при условии $x+y=0$.

Первый способ (метод множителей Лагранжа)

Обозначив $\varphi(x,y)=x+y$ составим функцию Лагранжа: $F(x,y)=z(x,y)+\lambda \varphi(x,y)=3y^3+4x^2-xy+\lambda(x+y)$.

$$ \frac{\partial F}{\partial x}=8x-y+\lambda; \; \frac{\partial F}{\partial y}=9y^2-x+\lambda.\\ \left \{ \begin{aligned} & 8x-y+\lambda=0;\\ & 9y^2-x+\lambda=0; \\ & x+y=0. \end{aligned} \right. $$

Решив систему, получим: $x_1=0$, $y_1=0$, $\lambda_1=0$ и $x_2=\frac{10}{9}$, $y_2=-\frac{10}{9}$, $\lambda_2=-10$. Имеем две стационарные точки: $M_1(0;0)$ и $M_2 \left(\frac{10}{9};-\frac{10}{9} \right)$. Выясним характер экстремума в каждой стационарной точке с использованием определителя $H$.

$$ H=\left| \begin{array} {ccc} 0 & \varphi_{x}^{"} & \varphi_{y}^{"}\\ \varphi_{x}^{"} & F_{xx}^{""} & F_{xy}^{""} \\ \varphi_{y}^{"} & F_{xy}^{""} & F_{yy}^{""} \end{array} \right|= \left| \begin{array} {ccc} 0 & 1 & 1\\ 1 & 8 & -1 \\ 1 & -1 & 18y \end{array} \right|=-10-18y $$

В точке $M_1(0;0)$ $H=-10-18\cdot 0=-10 < 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{\min}=0$. В точке $M_2\left(\frac{10}{9};-\frac{10}{9}\right)$ $H=10 > 0$, посему в данной точке функция имеет условный максимум, $z_{\max}=\frac{500}{243}$.

Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:

$$ d^2 F=F_{xx}^{""}dx^2+2F_{xy}^{""}dxdy+F_{yy}^{""}dy^2=8dx^2-2dxdy+18ydy^2 $$

Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

$$ d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2 $$

Так как $ d^2F \Bigr|_{M_1}=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F \Bigr|_{M_2}=-10 dx^2 < 0$, т.е. $M_2\left(\frac{10}{9}; -\frac{10}{9} \right)$ - точка условного максимума.

Второй способ

Из уравнения связи $x+y=0$ получим: $y=-x$. Подставив $y=-x$ в функцию $z(x,y)=3y^3+4x^2-xy$, получим некоторую функцию переменной $x$. Обозначим эту функцию как $u(x)$:

$$ u(x)=z(x,-x)=3\cdot(-x)^3+4x^2-x\cdot(-x)=-3x^3+5x^2. $$

Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.

$$ u_{x}^{"}=-9x^2+10x;\\ -9x^2+10x=0; \; x\cdot(-9x+10)=0;\\ x_1=0; \; y_1=-x_1=0;\\ x_2=\frac{10}{9}; \; y_2=-x_2=-\frac{10}{9}. $$

Получили точки $M_1(0;0)$ и $M_2\left(\frac{10}{9}; -\frac{10}{9}\right)$. Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак $u_{xx}^{""}$ в каждой стационарной точке или проверяя смену знака $u_{x}^{"}$ в найденных точках, получим те же выводы, что и при решении первым способом. Например, проверим знак $u_{xx}^{""}$:

$$u_{xx}^{""}=-18x+10;\\ u_{xx}^{""}(M_1)=10;\;u_{xx}^{""}(M_2)=-10.$$

Так как $u_{xx}^{""}(M_1)>0$, то $M_1$ - точка минимума функции $u(x)$, при этом $u_{\min}=u(0)=0$. Так как $u_{xx}^{""}(M_2)<0$, то $M_2$ - точка максимума функции $u(x)$, причём $u_{\max}=u\left(\frac{10}{9}\right)=\frac{500}{243}$.

Значения функции $u(x)$ при заданном условии связи совпадают с значениями функции $z(x,y)$, т.е. найденные экстремумы функции $u(x)$ и есть искомые условные экстремумы функции $z(x,y)$.

Ответ : в точке $(0;0)$ функция имеет условный минимум, $z_{\min}=0$. В точке $\left(\frac{10}{9}; -\frac{10}{9} \right)$ функция имеет условный максимум, $z_{\max}=\frac{500}{243}$.

Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака $d^2F$.

Пример №3

Найти наибольшее и наименьшее значения функции $z=5xy-4$, если переменные $x$ и $y$ положительны и удовлетворяют уравнению связи $\frac{x^2}{8}+\frac{y^2}{2}-1=0$.

Составим функцию Лагранжа: $F=5xy-4+\lambda \left(\frac{x^2}{8}+\frac{y^2}{2}-1 \right)$. Найдем стационарные точки функции Лагранжа:

$$ F_{x}^{"}=5y+\frac{\lambda x}{4}; \; F_{y}^{"}=5x+\lambda y.\\ \left \{ \begin{aligned} & 5y+\frac{\lambda x}{4}=0;\\ & 5x+\lambda y=0;\\ & \frac{x^2}{8}+\frac{y^2}{2}-1=0;\\ & x > 0; \; y > 0. \end{aligned} \right. $$

Все дальнейшие преобразования осуществляются с учетом $x > 0; \; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $\lambda=-\frac{5x}{y}$ и подставим найденное значение в первое уравнение: $5y-\frac{5x}{y}\cdot \frac{x}{4}=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $\frac{4y^2}{8}+\frac{y^2}{2}-1=0$, $y^2=1$, $y=1$.

Так как $y=1$, то $x=2$, $\lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.

$$ F_{xx}^{""}=\frac{\lambda}{4}; \; F_{xy}^{""}=5; \; F_{yy}^{""}=\lambda. $$

Так как $\frac{x^2}{8}+\frac{y^2}{2}-1=0$, то:

$$ d\left(\frac{x^2}{8}+\frac{y^2}{2}-1\right)=0; \; d\left(\frac{x^2}{8} \right)+d\left(\frac{y^2}{2} \right)=0; \; \frac{x}{4}dx+ydy=0; \; dy=-\frac{xdx}{4y}. $$

В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $\lambda=-10$, получив при этом:

$$ F_{xx}^{""}=\frac{-5}{2}; \; F_{xy}^{""}=-10; \; dy=-\frac{dx}{2}.\\ d^2 F=F_{xx}^{""}dx^2+2F_{xy}^{""}dxdy+F_{yy}^{""}dy^2=-\frac{5}{2}dx^2+10dx\cdot \left(-\frac{dx}{2} \right)-10\cdot \left(-\frac{dx}{2} \right)^2=\\ =-\frac{5}{2}dx^2-5dx^2-\frac{5}{2}dx^2=-10dx^2. $$

Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

$$ d^2 F=F_{xx}^{""}dx^2+2F_{xy}^{""}dxdy+F_{yy}^{""}dy^2=\frac{\lambda}{4}dx^2+10\cdot dx\cdot \frac{-xdx}{4y} +\lambda\cdot \left(-\frac{xdx}{4y} \right)^2=\\ =\frac{\lambda}{4}dx^2-\frac{5x}{2y}dx^2+\lambda \cdot \frac{x^2dx^2}{16y^2}=\left(\frac{\lambda}{4}-\frac{5x}{2y}+\frac{\lambda \cdot x^2}{16y^2} \right)\cdot dx^2 $$

Подставляя $x=2$, $y=1$, $\lambda=-10$, получим:

$$ d^2 F=\left(\frac{-10}{4}-\frac{10}{2}-\frac{10 \cdot 4}{16} \right)\cdot dx^2=-10dx^2. $$

Так как $d^2F=-10\cdot dx^2 < 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{\max}=10-4=6$.

Ответ : в точке $(2;1)$ функция имеет условный максимум, $z_{\max}=6$.

В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.